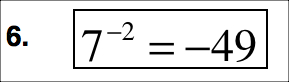More Tangrams Please!

This week in Geometry, we did the 3 Act lesson Hedge Trimmer. I'll debrief about that another time. Students needed to find the area of some isosceles trapezoids along the way and I didn't give them access to the area formula for trapezoids. Instead they needed to be resourceful and figure it out on their own. Well, that didn't go too well at first [cue the whining]. Many students had trouble breaking the trapezoid into 3 polygons: a rectangle and two triangles. Their warm-up the next day was to play around with tangrams for the first 5-10 minutes of class.

Me: Use all seven pieces to make any one of the following polygons. Do your best!

I drew a square, rectangle, trapezoid, parallelogram, triangle, and circle. I'm just kidding about the circle. However, I should have drawn one. That's funny. My 8th grade students were terrible at this. I use "terrible" with all the love in the world, knowing this is a learning experience for them.

Me: Have you guys ever messed around with tangrams?

Class: No!

Me: WHAT!!!! Are you guys serious? No one has ever let you mess around with tangrams before? Well, I'm glad we're doing it now. You guys need this. Seriously? You guys have never messed around with tangrams.

Class: Nope.

Me: Okay, well keep trying. [as I began scraping my jaw off the floor]

My request to you all: MORE TANGRAMS PLEASE!

Especially elementary teachers, more tangrams please. Have your students mess around with them. Sure you can download some app onto your tablet or find a web-based site to simulate tangrams, but please do your best to get actual tangrams into the hands of your students. Math formulas come and go for math students. However, if they can visually break apart polygons into more recognizable polygons such as rectangles and triangles, I believe their mathematical proficiency greatly increases. My goal is to get these 8th graders to play around with Tangrams once a week for the rest of the year. At least one of my students was eventually able to put together a trapezoid (top left), which quickly turned into a parallelogram, which quickly turned into a rectangle.

Me: How'd those other shapes come so quickly?

Sean: I just moved this one larger triangle to different spots.

I took a picture of his first configuration so I could share it with the class. I figured I'd give the class a chance to redeem themselves and copy his rectangle configuration.

More tangrams please! 

Repeat after me:

Thanks for listening.

Tangrams,
1104


BTW: Cheat sheet for displaying student work immediately:

1. Sign up for Dropbox.
2. Have the Dropbox app on your phone.
3. Take picture(s) of student work.
4. Allow the app to upload your camera photos.
5. Sync your computer with Dropbox.
6. The pictures arrive on your computer in seconds.

Wablammo!

Mistakes to the Half Power

Today, after completing Day 128 of Estimation 180, we briefly reviewed the first four questions of the handout from Day 1 of exponent mistakes. Read about Day 1 here. We then attacked the next four questions and each of my four Algebra sections had different ideas, explanations, successes, and challenges. It was beautiful.

Question 5 brought the best conversations of the day. Many students thought that 100 to the half power was 5000 because they went 100*50, thinking 100 should be multiplied by half of itself (50). There were two classes with one student in each that thought the answer was 10, but each student had a difficult time articulating their reasoning. Those two students weren't necessarily convinced with their answer either. I took the lead on this one after hearing this from a couple of students:

It can't be 5000, that's too high. It's gotta be somewhere between 1 and 100, but it isn't 50.

I wrote the following on the board:
100^3 =
100^2 =
100^1 =
100^0 =

Me: Do me a favor and evaluate each of those four expressions.

Respectively, students gave me:
100^3 = 1,000,000
100^2 = 10,000
100^1 = 100
100^0 = 1

It helped that we already proved a zero exponent simplifies to one. PHEW! So I stood there with a nondescript look on my face and asked students to make observations. They got my "What do you wonder? What do you notice?" face.

Me: Let's talk number sense here everyone. Where would we place 100 to the one-half power?

Many students quickly placed it between 100^0 and 100^1. So how is that 5000 looking? Does that make sense? Some keen observers (only a few throughout the day) noticed a pattern of decreasing zeros. One million decreases by two zeros to get ten thousand. Ten thousand decreases by two zeros to get one hundred and one hundred decreases by two zeros to get one. No one really said it was because they were dividing by 100 each time, but I let it slide. I didn't want to take anything away from some of the lightbulbs lighting up in class.

Sheena: Since you take away two zeros each time, and 100^1/2 is between 100^0 and 100^1, you only take away one zero to get 10.

Me: (to the class) What do guys think?

Class: Yea! Totally! That really makes sense.

Me: Is it enough to convince you all? Will this work every time? So let's try this:

I asked students for factors of 100. Students gave me:
50*2
10*10
4*25
10*100

Me: Which one of these is a perfect square?

Class: 10*10

Me: So let's rewrite 100 as 10^2 and keep the half power.

Class: Woah! It's ten to the first. So it's ten!

Me: So what can we conclude about something to the half power?

Student: It's the square root.

I toss up a couple expressions for confidence: 49^1/2. They shout, "seven!" or 64^1/2. They shout, "eight!" Now, if you want to really mess with some of your kids, throw 27^1/3 up on the board and ask, "So what is something to the one-third power?" You might get lucky with a kid that says 3. Maybe walk them through that one. For my honors kids, I would ask, "What number on the board is both a perfect square and perfect cube?" You know you have a smarty pants when they say 64. That's a gem right there. Don't expect that often in 8th grade. That's my Elijah! (the closest I'll get to Fawn's Gabe.)

Question 5 stole the show and our explanations for questions 6-8 were not as spectacular. That's fine. However, I think I'll switch the order of the questions and put this question #6 last (after current question #8). I found that the flow of explanations from students for current question #8 (quotient) really helped explore/explain negative exponents, making question #6 easier for students.

In one of my classes, Arielle came out of nowhere and gave us this gem. I immediately put it up on the Quotes of the Week board.

That's right! We're exploring these rules and students are defining them through observations and patterns. I think students have a better understanding of these properties and rules when given incorrect solutions (mistakes). In case I don't have time to wrap things up with you about tomorrow, the handouts from this week will be at the bottom of this post. Michael Pershan recommended I tell students that some solutions are incorrect and some are correct. I tried that out for Days 2 & 3. We only had about ten minutes to start today's handout. After their abbreviated individual time, I put these two things up on the board:

1. Share with your group the one solution you feel most confident about.
2. Select one question you want to know the answer to most.

I had students stand and vote once (by raising hand) for the question they wanted to know the answer to the most. I kept a quick tally. Most classes picked question #8. Still standing, I told students to either face the hallway if they thought the question was correct or face the windows (opposite the hallway) if they thought the question was incorrect. I take a quick tally. Sit back down and have students share out loud. I'd resume Fish Bowl if I had more time. Try this sometime. Fun. 

Tomorrow: more group work, less teacher. 

Half-power,

1002

Day 1 handout

Day 2 handout

Day 3 handout

Thank You Math Mistakes

Every year I dread teaching exponents like nothing else. I still do. It's one of those concepts (units) I have a tough time relating to, and if I have a tough time, imagine my students. For me, exponent rules and properties have been reduced to nothing more than a good puzzle. Not sure admitting that here is wise, but I do enjoy puzzles. However, to me, expressions with exponents don't necessarily lend themselves to having applied meaning for middle schoolers, or at least no simple contextual application I can relate with. This is where you jump straight to the comments and say something like,

"Andrew, exponents are seen in [insert awesome idea] and here's a link." or

"Mr. Stadel, students can relate to exponents when they [insert other awesome idea]." or

"Stades, I'm surprised you haven't done a 3 Act lesson on exponents using [insert other fabulous idea]."

"This year will be different." You ever mutter that to yourself? Well this year is and will continue to be. I shamelessly request you to temporarily stop reading this blog and visit Michael Pershan's website Math Mistakes. Seriously, type mathmistakes.org into your url address. The more I research teaching strategies and content, the more I'm starting to see the benefit of students learning math by identifying mistakes, correcting them, and justifying their reasoning while doing so. Inspired by Michael's post on exponents, here's the handout I threw at my 8th grade Algebra students today with the following directions:

The following statements are all INCORRECT.

1. Identify the mistake(s).
2. Correct.
3. Justify (show) your reasoning.

Me: I'll give you guys 3-5 minutes of individual time to work through as many questions as possible. Then you'll share and discuss your ideas with your group followed by a whole class discussion.

Students worked individually on the questions for a few minutes. When most students were at least 75% complete with the handout, I told them they had until the end of today's estimation song Can't Buy Me Love (in its entirety) to share their solutions and reasoning with their group members. I heard some great stuff. Next we did our Fish Bowl where students come up to the front, walk us through their work and reasoning on the board while we listen and watch both intently and quietly waiting to ask questions. Here's the four we got through today.

Students in the Fish Bowl identified the mistake as multiplying two by five, producing ten. Students also correctly explained how two to the fifth power is thirty-two. The fun part (for me) was seeing multiple representations. 

1. Common: 2*2 = 4, 4*2 = 8, 8*2 = 16, and 16*2 = 32.
2. Grouping two's so 2*2 = 4 twice. 4*4 = 16 and 16*2 = 32.

The mistake here was explained a few different ways, but mainly revolved around the student forgetting the negative.  So far, questions 1 and 2 have a lower entry point for today's task, considering these students haven't seen exponents since last year. Multiple representations looked like this:

1. Common: -2*-2*-2 = -8
2. Preferred: (-2)(-2)(-2) = -8

The classic. I always enjoy this example. Students explained that the mistake was made by multiplying -6 and -6, producing positive 36. Many students pointed out that the exponent is "attached" to the closest term (6) and not the entire expression (-6). Multiple representations included:

1. Common: -(6*6) = -36
2. Common: -6*6 = -36
3. Extra: -1*6*6 = -36

This was an extremely fun conversation to have in class. In fact, for some periods, we never established a conclusive answer to the question before the bell rang. Here's what they came up with. Some students simplified it to thirty-seven and many were convinced of this at first. Very few simplified it to one, but couldn't convince anyone why. Some students offered the following:

Joey: My fifth grade teacher told me anything to the zero power is one.

Raquel: There's some rule that says it's one. It's just the rule. 

Me: Who's convinced by their reasoning? No one? 

Here are the multiple student representations we saw:

1. Pattern: 37^2 = 37*37,  37^1 = 37, so 37^0 = 1 (this didn't convince many).
2. "Anything over itself is 1," some said. Therefore, 37^5 over 37^5 is one and you subtract the exponents (5-5) to get 37^0. Therefore, 37^0 = 1 (this convinced many).

I forgot to mention that before we did Fish Bowl, I asked students what was different about what they initially did with the handout. Here are a few things they said:

1. You gave us individual time instead of just going straight to group work.
2. We had to make corrections.
3. We had to try and figure out the questions without you telling us any rules.

The last observation was my favorite. This activity gave students a desire to listen to each other and want to know the answer to these questions. I wasn't at the front of the room blabbing out rules, properties, their names, and examples. I didn't provide students with guided practice. This combination of activities and strategies felt right. More to come tomorrow, but we can't ignore that there's something to this mistake idea. What do you think?

Mistakenly,

1227

*UPDATE: The next day does like this.

A Busy Week Paid Off

We have been really busy for the past couple of weeks preparing for an awesome opportunity, The 22nd Annual Fort Lauderdale International Auto Show. We had an awesome set-up thanks to a very generous company Regal Show Services that did and outstanding job organizing the Auto Show. 

We met Elliot Wachman at Broward County's Go Solar Fest. He felt like he could help us reaching our goal for this year's race. He along with Cliff Ray invited us to the auto show. As we were setting up we were amazed by the size plot Regal Show Service donated to our team. We had the same surface area as Jaguar, Subaru, and the Lexus LFA. We are so grateful for their help, we are still getting in donations and emails from the many contacts we made at the Fort Lauderdale International Auto Show.
Thank you Elliot and Cliff!

Capturing Time (musically)

Recently, I had the idea to do a theme of "song lengths" over at Estimation 180. Inspired by a recent comment from Fawn, I chose Santana's Oye Como Va. At first, I opened up iTunes and took a screen shot of the music player.  I threw in an album cover and edited it to look like this, asking "How long is Santana's Oye Como Va?":

I can get away with directly asking the question at Estimation 180. How would you make your estimate? I'd make my estimate based on the time played so far (1:26) and the location of the playhead in the timeline. I absolutely love that students have to use time here, specifically 60 seconds in a minute. Furthermore, I'm hoping students use some type of spatial reasoning with the timeline, either as a fraction, percentage, proportion, or something else. But that's it. Can we go anywhere else with this? This task feels constrained. This doesn't capture the medium of music correctly. There's got to be more, right?

The more I thought about it, I was curious of better ways (or the best way) to capture time and music. Let me rephrase that. If I were going for a more perplexing approach and wanted to create a 3 Act task to share at 101qs.com, how would I go about doing that? I remembered that I own the djay app and experimented with a really lengthy Jethro Tull song titled, Thick As A Brick. This is where I need your help. I'd appreciate you checking out Act 1 and letting me know the first question that comes to mind. Or watch it here and leave a comment/question in the comments.

Based on some initial questions, I'm thinking of revising Act 1 where the virtual record player looks more like this. (notice the record?)

The virtual record player opens up many possibilities with this task. There's a white tape marker on the record for precise tracking when playing the track. I feel there's a lot more math opportunities here, but at the same time it feels a little contrived?
Am I over-thinking this?
What do you see here?
What are your thoughts?
I need some help. Thanks in advance.

Spin it,
339

Buses [Day 2]

Woah!!! We saw six buses today on our way to preschool. You might want to check out the Buses [Day 1] post from two days ago to understand the context of what's ahead. I was a little late to the bus-counting action on our way to preschool today so here's our first exchange.

Me: Have you seen any buses today?

Son (who turns 3 in a month): Yes. One.

Me: Was it a city or school bus?

Son: City. 

Me: Okay, we'll have to look for more buses today.

We immediately saw another city bus, bringing our total buses to two on the day. A little bit down the road was another city bus heading in the oposite direction.

Me: I see something on the other side of the road coming this way. What is it?

Son: It's another bus!! A city bus!

Me: How many total buses have we seen today? 

Son: Three.

Me: Good.

We continue along and a shorter city bus passes us. I don't point it out, but he spots it.

Son: There's another bus. 

Me: You're right. Wow! Now, how many buses have we seen?

Son: Hmph.

I pause and wait for him to process the question. Keep in mind, this is happening while I'm driving and he's in the backseat so I can't turn around to talk with him.

Son: Hmph

If I get a second "hmph" I know he doesn't have an answer and won't come up with one. Trust me, I've waited for long periods of time and will just continue to hear his cute little "hmph."

Me: Well, we already saw three buses and now we saw one more. What number comes after three?

Son: (whispering to self: one, two, three) Four.

Me: Good. So how many buses have we seen?

Son: Four.

Surprisingly, we hadn't seen a school bus yet. We were at our last red light and there it was in all its glorious mustardy-yellowy paint, a school bus. He exclaims, "A school bus!" Since we're at a red light, I turn around and ask how many buses have we seen. I get the two "hmph" count. I hold up one hand with four fingers up and the other hand with one finger up.

Me: We saw four city buses and now one school bus. How many buses have we seen today?

Son: Three

Did we just have a flashback (regression) to Tuesday?

Me: We did see three buses today, you're right. But, I think we've seen more. Count the fingers.

Son: One,... Two,... Three,... Five.

The light turns green and I have to go. I'm curious about him skipping 'four' and still landing on the correct number of buses. Seriously, what's up with that? I mumble to myself, "That's odd that he skipped four." Right as we're about to pull into the preschool parking lot, another school bus goes whizzing by in the opposite direction. He exclaims, "Another school bus!" Wow! We saw six school buses today, so I'm thinking we park the car and quickly review this last school bus.

Me: Wow! We just saw another school bus. We saw a lot of buses today. We saw five buses and now we saw one more. How many total buses did we see today?

Son: Hmph. (x2)

I hold up one hand with all five fingers up and the other hand with one finger up.

Me: So we saw five buses and we just saw another bus. Count the fingers.

Son: One,... Two,... Three,... Four,... Six.

Me: You're right. What happened to five?

He giggles! I do too because it's contagious. Seriously, what's up with this? He answered the correct number, but skipped the number directly preceding it. TWICE! He's happy he saw so many buses today. I am too. He's content with landing on the correct number. I'm perplexed.

Hmph,
1140

BTW. Thanks Christopher Danielson, for continuing to inspire me to have (and cherish) these conversations with my son.

Setting Up

We have been really busy for the past couple of weeks preparing for an awesome opportunity, The 22nd Annual Fort Lauderdale International Auto Show. This event will hopefully bring in many connections and sponsors throughout the automobile industry and the community. This support will help us raise our goal of $30,000 for our upcoming cross-country race this summer, Texas to California. We are the ONLY solar racing team in Florida to participate in a national race in both the high school and university level! 

Please come visit our booth at The Fort Lauderdale International Auto Show 

@ the Broward County Convention Center. 

The show dates and times are: 

Thursday      April  4th        3:00pm      to    10:00pm

Friday          April  5th        3:00pm      to    11:00pm

Saturday      April  6th        10:00am     to    11:00pm

Sunday        Apri l 7th        10:00am     to    8:00pm

Our booth is located by the entrance of HALL A 

 Solar Knight I, this is the car that started it all!

Solar Knight III, the most expensive, the fastest, the most advance!

 Kavita (Freshman) with her parents making sponsor portfolios.

 Some last minute polishing to SKIII.

Our Awesome Display Board! 

We brought our robotics "play pin" to demonstrate team collaboration between South Plantation's Engineering Program, Solar/Robotics.

Dancing with the Functions

I'm honored and humbled to have been a (small) part of Christopher Danielson's online course The Mathematics in School Curriculum: Functions. There were some great tasks, discussions, and contributors. I now have a better misunderstanding of functions. However you interpret that last sentence, let me assure you that this two week course broke me down in order to give me a better perspective and idea of functions. Professor Triangleman moderated the course well, provided challenging tasks and opportunities that took me out of my comfort zone, encouraged us to think differently, and didn't hesitate to whip us into shape as you can see here:

He's referring to beating me down while informing the teacher's pet (Fawn) of his tactic.

Our choices for our final project were:

• a blog post,
• a lesson plan,
• an interpretive dance,
• a work of visual art,
• etc.

I thought writing a blog post was "too easy" in the sense that I could blog about anything ordinary at anytime. This class wasn't ordinary though, and I felt I'd rather try and give something back to the class, professor, and community in exchange for what I have received. No Fawn, not because I'm "too lazy." Therefore, I'm going to give you a lesson idea I have, based on an interpretive dance, which might be a work of visual art, all wrapped up in a blog post.

Interpretive dance really got me thinking. I thought back to the handful of dance lessons my wife (fiance at the time) and I took to practice for the First Dance at our wedding. My wife was a natural. As for me, well let's just say all the dance lessons in a lifetime wouldn't have helped. Here's a dance photo I have of us where it actually looks like I'm doing something worthy. Don't be fooled.

Don't worry, I won't torture you with video. Anyway, our dance instructor taught us many helpful tips and gave us a glimpse of dances like swing, salsa, the waltz, and the two-step box. We only did a few moves in our wedding dance, but it mainly revolved around the two-step box. We had a short song, thank goodness. I'm sure our guests would have taken their gifts back had they seen me dance any longer.

Here comes my lesson idea. I'd like to see the relationship between the number of steps taken in a dance over time. So let's make it a graphing story. Here's the first 30 seconds of a dance. Write a story for it. Even better, can you write the functions (along with any intervals, domains, ranges, etc)? Go here to Desmos to check your answers. I give you my interpretive dance.

Thanks to Sadie, Timon, and Michael Pershan for inviting me to their hangouts. I was honored to collaborate with you guys during one of the hangouts and bounce ideas off of each other. Thanks to Fawn for getting me in trouble, ratting me out to the teacher, and reminding me to submit my final project. Where would I be without you? Probably in class and not in the principal's office.

I would love some feedback on this lesson idea. Would you have your students dance? If so, what dance(s)? Would you have students come up with a function for each type of dance? What kind of relationships would you have your students look for? Would you consider "dancing" an applicable use of functions? I leave you with this clip. You must give these guys (Sean and John Scott) some crazy respect. They're insanely fantastic at tap-dancing. Just watch the first minute. Then make a graphing story.

Dance,
933

Buses

I just returned from taking my son (turns 3 in a month) to preschool. One of the many perks to Spring Break so far! On the way to preschool, my son spotted a city bus.

Son: Ohhhh! A bus!

Me: Right. What type of bus? 

Son: A city bus. 

A little background knowledge here: He loves trucks! Let me rephrase that. He loves anything larger than a car, has an engine, is big, makes a lot of noise, is big, does construction, is big, intakes diesel, etc. I've seen many kids share these interests, especially when the garbage man does his rounds in our neighborhood. You'd think the garbage man was passing out ice cream or something (and he doesn't need that silly Ice Cream truck music either). We have multiple truck books that get frequent use before nap and bedtime. We have a surplus of toy trucks and Legos, recently added to by the most generous, wonderful, and great Fawn. You're the best!

Back to our drive. We had just stopped at a red light and on the other side of the street he spots a school bus.

Son: Ohhh! A school bus!

Me: You're right!

Son: We've seen two buses!

Me: I know. Look what's coming up behind the school bus.

Son: Another bus.

Me: And what type of bus is that?

Son: A city bus.

Me: So how many buses have we seen?

Son: Three!

Me: That's right. We've seen 2 city buses and 1 school bus, so we've seen a total of...

I pause for him to fill in the blank.

Son: Three!

We're still stopped at the red light and have a little time before the green light. I turn around and illustrate this again with my fingers, because lately he's been doing really well identifying the numbers one through five on a single hand. Since we saw two different types of buses, I use two hands. I hold up on hand with two fingers up and say, "We've seen two city buses" and on the other hand I hold up one finger saying, "and we've seen one school bus. So we've seen a total of how many buses?"
I expect him to say "three" because it's fresh in his mind, but he pleasantly surprises me and I can see his eyes moving across my fingers and mentally counting the fingers to verify the word 'three' matches up with Dad's fingers. "Three." he says.

The light turns green and we're on our way. We have less than five minutes until we get to preschool. Of course, I'm keeping my eyes peeled for more buses. No buses. Shucks. However, we pull into the parking lot of the preschool and park. Before I exit the car to get him out, I turn around and want to try something. Simply for fun.

Me: So we saw two city buses [I'm holding up two fingers on one hand]. What if we saw two school buses [I hold up two fingers on my second hand]. How many buses would we have seen?

Son: Three.

Me: Are you sure? Count my fingers.

Son: One... two... three... four, five, six, seven, eight, nine, te...

Me: Okay, silly. [holding up two fingers on each hand again] If we saw two city buses and two school buses, how many total buses would we see?

Son: Three.

I left it at that. He's content with the concrete. It's not about future counting for him. It's about what he just experienced, what's relevant, what's applicable and what's associated with his interests. I made a small attempt at the abstract, just for fun. There's no need to push this any further. He's convinced we saw three buses and he's right. He doesn't care about a fourth bus that we didn't see. Plus, it's time for preschool. Man, I love vacation. I get to have conversations like this with my son. It doesn't get any better than that.

Buses,
1047

[UPDATE]
*Read what happened two days later in Buses [Day 2].

Not Drawn to Scale

I hope you'll allow me to vent for a bit. I have been encouraging my students to be in tune with the 8 Mathematical Practices by Standard of the CCSS for some time now. It's pretty safe to say that my students know I really favor Mathematical Practice Standard 6, Attend to Precision. However, some of the resources I occasionally use in class are beginning to play tricks with everyone's minds, including mine. Here's a resource I have, Cooperative Learning and Geometry by Becky Bride.

Don't get me wrong, I like this book. It has some great explorative exercises that have appropriately challenged my students. For example, look at this exercise to help students derive the 30-60-90 triangle relationships. Take an equilateral triangle, its altitude, and the Pythagorean Theorem to find out the special relationships between the shorter leg, longer leg, and hypotenuse. Great.

Here's where I start to beat my head against the wall. The book uses diagrams that simply shouldn't be used, especially in the context of 30-60-90 triangles. Look closely...

That's right, the 30 degree angle is opposite the longer (drawn) leg for questions 1, 3, and 4. My students get bothered by this contradiction. I do too. I have no problem admitting this to them. I'm honest with them saying, "I know guys. It goes against everything we strive to do in here. I encourage you guys to attend to precision and check for reasonableness. Yet, I give you this. I'm sorry. It says at the top 'not drawn to scale', but they should be drawn to scale. Right guys?!"

I think this about sums it up. Students will come up and ask about the dimensions they've solved for and whether or not they're reasonable. I'm proud of my students for making sense of their answers and checking for reasonableness.  I know something is a skew when my response to those students is,

"I never assume those things are drawn to scale." 

I feel rotten saying this to students. I feel like I've just provided them with a worthless and menial task. I've let them down. I feel dirty. Mr. Stadel's quality control group hasn't done their job. What message are we sending students? Do they think we're out to trick them? Do the directions read, "Find the mistakes?" They should. It's times like these that force me to (gladly) keep a closer eye on the content I provide my students with. Don't just throw some triangles at them with random angles and units. Make sure they're reasonable.

Have you ever felt this way? Have you ever been caught in this situation? What did you do? How do we avoid these situations again? How do we demand better quality content from publishers? How do we make sure we provide our students with content that matches the CCSS and Mathematical Practices? Maybe you're okay with these types of diagrams, so please explain why. I want to hear from you all on this.

nOt tO sCAlE,
939