Stretch
I am reluctantly pressing "publish" for this post. However, please know that the rawness and honesty in this post is aimed at making each and every one of us better at what we (both individually and collectively) do to support our students.
Kate wrote a great post the other day about some teachers coming out of TMC14 feeling inadequate. I support Kate's attitude and conclusion:
I started learning and exploring how to play the guitar in high school. I stunk. My family probably got tired of me playing Deep Purple's Smoke on the Water and Metallica's Enter Sandman all day. The first two riffs (and eventually songs) I learned. However, I practiced. A LOT. When I wasn't playing basketball, I practiced guitar. When I was supposed to be doing homework, I practiced guitar. There were guys at my high school who played guitar and were better. It made me practice more. It made me want to be better at something I loved doing.
When I got into college, my focus on guitar playing was similar. I was a lot better by this time, but still practiced a lot. When I wasn't working or going to class, I practiced guitar. When I was supposed to be studying, I practiced guitar. Then I joined a few bands and we practiced a lot. Not only did I continue practicing by myself, but now I practiced with others. That's awesome. We got better together! I would also jam with other guitarists who were better than me. Sometimes they were better so I learned a lot. Sometimes, I was better so I got to share some things and could relate. Every time I jammed with someone, it was a chance for me to improve at something I loved doing.
I loved going to concerts or watching videos of my favorite guitarists like Jimi Hendrix, Eric Clapton, or Warren Haynes. I wanted to cut my hands off many times because there was no way I would ever be as good as them. However, it only made me want to learn from them, steal some of their licks (guitar moves/techniques), and be the best I could be with their help and inspiration. I remember meeting James Hetfield from Metallica and was star struck. I thanked him for his inspiration. That's all I could muster up the intelligence to say. If I could jam with him I'd probably mess up A TON! But I'd never turn that opportunity down, because I'd learn a lot and he'd push me to get better.
Once during college, I was in Chicago at Kingston Mines blues bar hanging with my cousin. This blues/funk band, Charlie Love, was up there laying down some great songs. I went up at their break to compliment them and they invited me up to do a funk jam with them. I was completely honored and humbled at the same time. Here is this tall white guy trying to play funk with the Chicago blues/funk band and I did not play as well as I could have. However, I was grateful to meet them, I learned a lot from watching them, and it again made me want to go home and practice until my hands fell off.
For me, this connects so well with where I am as a math teacher. I am grateful for many other math teachers who have inspired me. There are many times I feel inadequate. Maybe I've met some of these math teachers and I feel like my brain shuts down. The best I can utter is some number and ignorantly nod my head in agreement. However, meeting inspiration and hanging out with inspiration has made me want to become a better teacher for my students.
Imagine there was an opening at your school and you could hire your teaching colleague. Would you turn down the chance to work alongside:
I recently offered a keep-your-head-up comment somewhere saying,
210
Kate wrote a great post the other day about some teachers coming out of TMC14 feeling inadequate. I support Kate's attitude and conclusion:
We are all good at some things and suck at other things. One thing we all share is the recognition that we all have work to do, and that we can all get better, and that focusing on that is worth our time.I believe we need inadequacies and need to feel them at times because they make us better at what we're striving to be: the best teacher for our students. We don't need inadequacies to feel inferior to other teachers or generate some type of MTBoS worth. Here's how I think we all need inadequacies.
I started learning and exploring how to play the guitar in high school. I stunk. My family probably got tired of me playing Deep Purple's Smoke on the Water and Metallica's Enter Sandman all day. The first two riffs (and eventually songs) I learned. However, I practiced. A LOT. When I wasn't playing basketball, I practiced guitar. When I was supposed to be doing homework, I practiced guitar. There were guys at my high school who played guitar and were better. It made me practice more. It made me want to be better at something I loved doing.
When I got into college, my focus on guitar playing was similar. I was a lot better by this time, but still practiced a lot. When I wasn't working or going to class, I practiced guitar. When I was supposed to be studying, I practiced guitar. Then I joined a few bands and we practiced a lot. Not only did I continue practicing by myself, but now I practiced with others. That's awesome. We got better together! I would also jam with other guitarists who were better than me. Sometimes they were better so I learned a lot. Sometimes, I was better so I got to share some things and could relate. Every time I jammed with someone, it was a chance for me to improve at something I loved doing.
I loved going to concerts or watching videos of my favorite guitarists like Jimi Hendrix, Eric Clapton, or Warren Haynes. I wanted to cut my hands off many times because there was no way I would ever be as good as them. However, it only made me want to learn from them, steal some of their licks (guitar moves/techniques), and be the best I could be with their help and inspiration. I remember meeting James Hetfield from Metallica and was star struck. I thanked him for his inspiration. That's all I could muster up the intelligence to say. If I could jam with him I'd probably mess up A TON! But I'd never turn that opportunity down, because I'd learn a lot and he'd push me to get better.
Once during college, I was in Chicago at Kingston Mines blues bar hanging with my cousin. This blues/funk band, Charlie Love, was up there laying down some great songs. I went up at their break to compliment them and they invited me up to do a funk jam with them. I was completely honored and humbled at the same time. Here is this tall white guy trying to play funk with the Chicago blues/funk band and I did not play as well as I could have. However, I was grateful to meet them, I learned a lot from watching them, and it again made me want to go home and practice until my hands fell off.
For me, this connects so well with where I am as a math teacher. I am grateful for many other math teachers who have inspired me. There are many times I feel inadequate. Maybe I've met some of these math teachers and I feel like my brain shuts down. The best I can utter is some number and ignorantly nod my head in agreement. However, meeting inspiration and hanging out with inspiration has made me want to become a better teacher for my students.
Imagine there was an opening at your school and you could hire your teaching colleague. Would you turn down the chance to work alongside:
- Dan Meyer because of his 3-Act creativity?
- Steve Leinwand because he's the Tasmanian Math-devil challenging you to be your best?
- Fawn Nguyen because she cusses and can't afford to not help her students do amazing things.
- Karim Ani because he looks at the world in interesting ways to tell stories and use math to serve them?
- Kate Nowak because she's pioneered blogging and has crazy-cool math stuff?
- Matt Vaudrey because he's willing to grow (or wear) a mullet for a ratios lesson?
- Cathy Yenca or John Stevens because they're integrating 21st century skills in their classrooms?
- Robert Kaplinsky because he writes detailed and amazingly cool PBLs?
- insert name because they inspire you and make you want to be a better teacher?
I recently offered a keep-your-head-up comment somewhere saying,
"Think of the skills you will acquire when making changes."My challenge to you (and myself), if you're feeling inadequate or inferior at any time is to:
- take risks
- be brave
- tap into your influences and inspirations to stretch yourself
- be the best teacher for YOUR students, not the MTBoS.
210
San Diego Conversions
I was in San Diego, California the past few days doing the whole San Diego Zoo and SeaWorld thing with the family. We had a great time, but that's not the point of the post. There were definitely a handful of opportunities to capture some math moments, but I've found it more important to contain myself (mathematically) when I'm with family and make the most of our time together. Here are the two things I captured and want to share.
Number 1:
We were waiting to board the Wild Arctic Ride (virtual helicopter ride) at SeaWorld and watched this video. There were subtitles in Spanish for our spanish-speaking (reading) friends. However, they go along with the helicopter pilot.
Here's Act 1:
When I saw the the number behind the black box, I thought, "Is that right? Is 400 miles per hour really ### kilometers per hour?"
Are they correctly converting for our Spanish speaking friends? It turns out that 400 miles per hour is about 643.7 kilometers per hour.
Here's act 3:
What do you think? Should I keep the black box there? Should I delete it?
I feel this is one of those moments where I don't insert a black box and we simply ask students:
Is 400 miles per hour really 600 kilometers per hour?
I'm curious about students arguing about this one? or would they even care?
What difference would 40 kilometers per hour make?
Where do you stand, on any of it?
Number 2:
The great thing about San Diego is there are tons of people from many different places of the world. San Diego has an international airport and many places of interest besides SeaWorld and the zoo to contribute to this melting pot. I loved listening to all the different languages being spoken throughout the day. Therefore, it didn't surprise me when I walked into the pool area for the first time on our trip and noticed a few interesting things. I couldn't help but think how wonderful it would be to use these in any math classroom, specifically Math 6. The first thing you see as you enter the pool area is the jacuzzi. I couldn't help but notice the depth:
Okay class, check this conversion. It ends up making sense and I appreciate the use of meters for pretty much everyone outside of the United States. Seriously, I simply have such a hard time understanding why the United States uses inches, feet, yards, miles, etc. I digress.
Here's the (very shallow) pool:
Let's look a little closer at the depth signs around the pool. The deepest part of the pool is 4 feet or 1.2 meters. Okay class, check this conversion. Looks pretty legit, right?
So, if you saw a depth sign with 3.5 feet, what would you put the meters conversion at? How would you order these pictures with your students? Which would you present first? second? third? or would you give them all to your students at the same time? Would you cover up one of the measurements (like feet) and only show them one measurement so they work on finding the conversion. Here's the 3.5 ft depth sign.
Okay, if you do the conversion, 3.5 feet is 1.0668 meters. Obviously, someone was following their rounding rules. A few questions pop into mind here:
Should we round up?
Would it be wiser to round to 1 meter?
How much of a difference does roughly 4 centimeters make?
Could they not use a slightly larger tile and put 1.07 meters?
These questions aren't the only questions, nor the most profound, but I'm still curious.
There's one more crazy thing about this pool I had to capture and share. How did they get away with this?
Look closely. Inside the pool is a depth of 4 feet (1.1 meters). Outside the pool is a depth of 3.5 feet (1.1 meters). WHAT?!!! Now reflecting, I should have had my wife take a picture of me next to the sign to get the water level and measure how deep it actually is here. I don't know about you, but 6 inches is definitely more significant than the 4 centimeters we discussed earlier.
At what point does an error like this matter significantly enough to change it? 6 inches? 2 inches? 12 inches? and in what direction: shallower or deeper?
How would you use any of these images or video in your class to help facilitate discussions or arguments regarding conversions?
SD conversions,
906
Number 1:
We were waiting to board the Wild Arctic Ride (virtual helicopter ride) at SeaWorld and watched this video. There were subtitles in Spanish for our spanish-speaking (reading) friends. However, they go along with the helicopter pilot.
Here's Act 1:
When I saw the the number behind the black box, I thought, "Is that right? Is 400 miles per hour really ### kilometers per hour?"
Are they correctly converting for our Spanish speaking friends? It turns out that 400 miles per hour is about 643.7 kilometers per hour.
Here's act 3:
What do you think? Should I keep the black box there? Should I delete it?
I feel this is one of those moments where I don't insert a black box and we simply ask students:
Is 400 miles per hour really 600 kilometers per hour?
I'm curious about students arguing about this one? or would they even care?
What difference would 40 kilometers per hour make?
Where do you stand, on any of it?
Number 2:
The great thing about San Diego is there are tons of people from many different places of the world. San Diego has an international airport and many places of interest besides SeaWorld and the zoo to contribute to this melting pot. I loved listening to all the different languages being spoken throughout the day. Therefore, it didn't surprise me when I walked into the pool area for the first time on our trip and noticed a few interesting things. I couldn't help but think how wonderful it would be to use these in any math classroom, specifically Math 6. The first thing you see as you enter the pool area is the jacuzzi. I couldn't help but notice the depth:
Okay class, check this conversion. It ends up making sense and I appreciate the use of meters for pretty much everyone outside of the United States. Seriously, I simply have such a hard time understanding why the United States uses inches, feet, yards, miles, etc. I digress.
Here's the (very shallow) pool:
Let's look a little closer at the depth signs around the pool. The deepest part of the pool is 4 feet or 1.2 meters. Okay class, check this conversion. Looks pretty legit, right?
So, if you saw a depth sign with 3.5 feet, what would you put the meters conversion at? How would you order these pictures with your students? Which would you present first? second? third? or would you give them all to your students at the same time? Would you cover up one of the measurements (like feet) and only show them one measurement so they work on finding the conversion. Here's the 3.5 ft depth sign.
Okay, if you do the conversion, 3.5 feet is 1.0668 meters. Obviously, someone was following their rounding rules. A few questions pop into mind here:
Should we round up?
Would it be wiser to round to 1 meter?
How much of a difference does roughly 4 centimeters make?
Could they not use a slightly larger tile and put 1.07 meters?
These questions aren't the only questions, nor the most profound, but I'm still curious.
There's one more crazy thing about this pool I had to capture and share. How did they get away with this?
Look closely. Inside the pool is a depth of 4 feet (1.1 meters). Outside the pool is a depth of 3.5 feet (1.1 meters). WHAT?!!! Now reflecting, I should have had my wife take a picture of me next to the sign to get the water level and measure how deep it actually is here. I don't know about you, but 6 inches is definitely more significant than the 4 centimeters we discussed earlier.
At what point does an error like this matter significantly enough to change it? 6 inches? 2 inches? 12 inches? and in what direction: shallower or deeper?
How would you use any of these images or video in your class to help facilitate discussions or arguments regarding conversions?
SD conversions,
906
OLDTIMER GP AUG 8-10
next week i will be at the OLDTIMER GP AT THE NURBURGRING AUG 8-10
Stop on by the Porsche stand and say hi
67s final fit
Final fit -a few last minute additions and it's off to paint next week - now all I need to do is nail down the final color
On our way to Austin,TX
It was the last day of the race as we said our goodbyes to Baylor University. Dr. Marx greeted us in the morning and waved us off the start to our final stop in Austin TX.
The finish line of the race was the Samsung Microprocessor factory in Austin TX.
Our over 300 mile journey had come to a close and we received our 3rd place trophy that night at the banquet. We also received the Matt Tunnel award for the most prestigious skill in driving and trailering.
On the road rally to Waco!
It was the morning of the the first road rally day and we were pumped up and ready to go.
By winning the previous days race we got the trophy at the flip of a coin from having a tie number of laps as staten island. We charged our batteries in the sunlight and suited Matt up in his cool shirt vest for the long trek ahead. Our destination for that day was Waco TX which was over 100 miles away.
We completed 98 miles that day and arrived in Waco Texas long enough to adjust our charge controllers and get some well earned sleep.
chris forsberg -garage tours show
CHAMPION PRO FORMULA-D - DRIFTER,MOTORHEAD AND ALL ROUND COOL DUDE CHRIS FORSBERG STOPPRD BY THE GARAGE TO FILM A SEGMENT FOR HIS #GARAGETOURS SHOW -
HE EVEN GOT BEHIND THE WHEEL OF CAR # 277 CHECK IT OUT
MANY THANKS TO : Formula Drift star @chrisforsberg64 and @NetworkA
Des-man
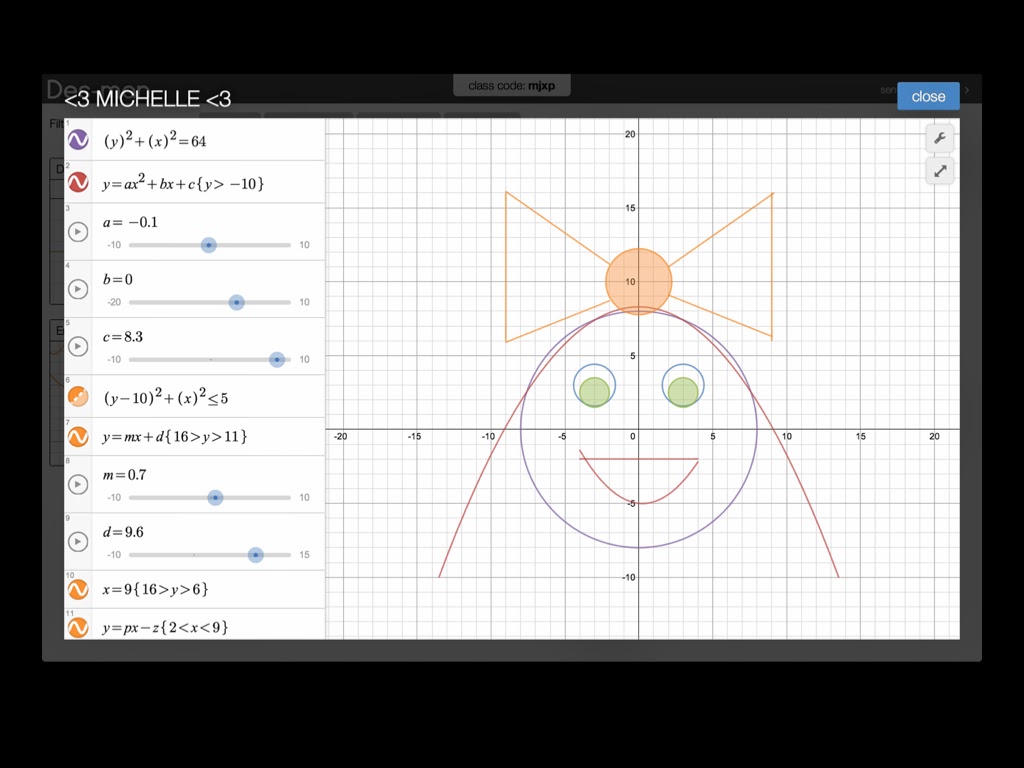
Today, students had about 90 minutes to work on creating their Des-man. Des-man was the brainchild of Fawn. Desmos then teamed up with Dan Meyer and Christopher Danielson to create a suite of classroom activities, one of them being Des-man. I've done Des-man before, but not with the Desmos classroom. Let me just say, it's awesome!
As the teacher, I could see every students' work in real-time and display it up on the projector for all to see if need be. That's a really slick feature on top of the already amazing Desmos. It's like math euphoria! It was a blast to see students work 90 minutes straight, being as creative as possible with their Des-man (or Des-woman). After three weeks, Desmos became a very familiar tool for students because they used it with tasks like Barbie Bungee, Datelines, Hit the Hoop, Vroom Vroom, Stacking Cups, and more. I'd like to showcase a few creations for you. Enjoy!
Thanks Fawn, Desmos, Dan, and Christopher for a wonderful and creative math experience. Lastly, I want to thank my students. Today, you guys helped each other out, persevered, asked for advice, freely explored, had fun, and wanted to know more about functions, domain, range, circles, sliders, and more!
Desmos is great about asking for feedback. I have some observations and am curious. Maybe I'm missing something, but I noticed some features from the regular desmos calculator missing in the classroom. Maybe these are upcoming features:
Students couldn't duplicate functions. How come?
Students couldn't create (use) tables. How come?
Students couldn't create folders or text boxes. How come?
Students can't share their Des-man (email, link, etc.). How come?
As the teacher, I can't keep the Des-man (functions included) for each student. How come?
As the teacher, I'd love to have access to each student Des-man, especially if I want to send it to that student or share at a later time.
Thanks for listening, Desmos!
Des-manian,
1035
As the teacher, I could see every students' work in real-time and display it up on the projector for all to see if need be. That's a really slick feature on top of the already amazing Desmos. It's like math euphoria! It was a blast to see students work 90 minutes straight, being as creative as possible with their Des-man (or Des-woman). After three weeks, Desmos became a very familiar tool for students because they used it with tasks like Barbie Bungee, Datelines, Hit the Hoop, Vroom Vroom, Stacking Cups, and more. I'd like to showcase a few creations for you. Enjoy!
Thanks Fawn, Desmos, Dan, and Christopher for a wonderful and creative math experience. Lastly, I want to thank my students. Today, you guys helped each other out, persevered, asked for advice, freely explored, had fun, and wanted to know more about functions, domain, range, circles, sliders, and more!
Desmos is great about asking for feedback. I have some observations and am curious. Maybe I'm missing something, but I noticed some features from the regular desmos calculator missing in the classroom. Maybe these are upcoming features:
Students couldn't duplicate functions. How come?
Students couldn't create (use) tables. How come?
Students couldn't create folders or text boxes. How come?
Students can't share their Des-man (email, link, etc.). How come?
As the teacher, I can't keep the Des-man (functions included) for each student. How come?
As the teacher, I'd love to have access to each student Des-man, especially if I want to send it to that student or share at a later time.
Thanks for listening, Desmos!
Des-manian,
1035
Quest For The Checkered Flag!
We raced all day and took a 30 minute break to take the official race picture.
Tools: Helpful & Unhelpful
Not sure I made the best teaching move today, but I had to try it. We explored Dan Meyer's "Will it hit the hoop?" task(s).
Act 1: Roll "Take 1"
I typically ask students to think of information they would find useful in answering the question. Today, I went somewhere else with Mathematical Practice 5. I asked students to make two lists:
I love how some students thought Desmos would be helpful, while others thought it'd be unhelpful. Those that found it unhelpful, wished you could insert images into Desmos so they could use sliders to find the path of Dan's shots. Boy, were they happy when they discovered you could import images. My first class was split down the middle: half thought slope-intercept might be useful and half didn't. It took a few convincing students to explain why Vroom Vroom was an example where a linear function was unhelpful.
Overall, I'm pleased with this approach, but I wouldn't do it with every task. It might confuse students that there's only one way to solve a task and detract from the importance of MP 5. I thought this was a fitting opportunity for students to mainly see the difference between a linear function and quadratic function. Specifically, I wanted them to see the advantages of using sliders in Desmos with a quadratic function instead of a linear function. I think students need to shuffle through their tool belt often and pick the right tools for the right task. I think today it was necessary. Dan has written about this or breaking students' tools. Moving forward, it's a matter of using this strategy at relevant times and not overusing it. However, I might be wrong altogether. That's where it's your turn to chime in...
Tomorrow: Des-Man!
Tools,
1125
Act 1: Roll "Take 1"
- Agree on the question, "Will he make the basketball shot?"
- Ask students to make a series of guesses for a total of six takes.
I typically ask students to think of information they would find useful in answering the question. Today, I went somewhere else with Mathematical Practice 5. I asked students to make two lists:
- List 1: Math tools that would be UNhelpful.
- List 2: Math tools that would be helpful.
- Class height: Measurement, mean, median, mode, range
- Number Tricks: inverse operations
- Bucky the Badger: Tables
- Barbie Zip Line: Pythagorean Theorem, wrong models
- Taco Cart: Pythagorean Theorem
- Barbie Bungee: Measuring, Data collecting, Tables, Line of best fit, slope-intercept, Desmos
- In-N-Out Burger: Slope-Intercept, Functions
- Styrofoam Cups: Functions, slope-intercept
- Stacking Cups: functions, slope-intercept, Desmos
- Basketball shots: guess and check, tables, linear systems, Desmos
- Datelines: functions, Desmos, linear inequalities
- Vroom Vroom: Measuring, Data collecting, Desmos, function of best bit, quadratic equations
I love how some students thought Desmos would be helpful, while others thought it'd be unhelpful. Those that found it unhelpful, wished you could insert images into Desmos so they could use sliders to find the path of Dan's shots. Boy, were they happy when they discovered you could import images. My first class was split down the middle: half thought slope-intercept might be useful and half didn't. It took a few convincing students to explain why Vroom Vroom was an example where a linear function was unhelpful.
Overall, I'm pleased with this approach, but I wouldn't do it with every task. It might confuse students that there's only one way to solve a task and detract from the importance of MP 5. I thought this was a fitting opportunity for students to mainly see the difference between a linear function and quadratic function. Specifically, I wanted them to see the advantages of using sliders in Desmos with a quadratic function instead of a linear function. I think students need to shuffle through their tool belt often and pick the right tools for the right task. I think today it was necessary. Dan has written about this or breaking students' tools. Moving forward, it's a matter of using this strategy at relevant times and not overusing it. However, I might be wrong altogether. That's where it's your turn to chime in...
Tomorrow: Des-Man!
Tools,
1125
Subscribe to:
Comments (Atom)